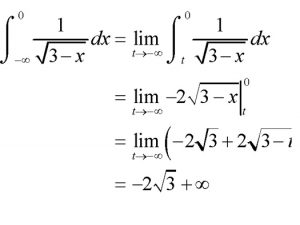Belirli ve Belirsiz İntegral Hesaplama Yöntemleri

Görüntülenme: 205

0

Okuma Süresi:3 Dakika, 17 Saniye

BELİRLİ VE BELİRSİZ İNTEGRAL
HESAPLAMA YÖNTEMLERİ

I. BELİRSİZ İNTEGRAL
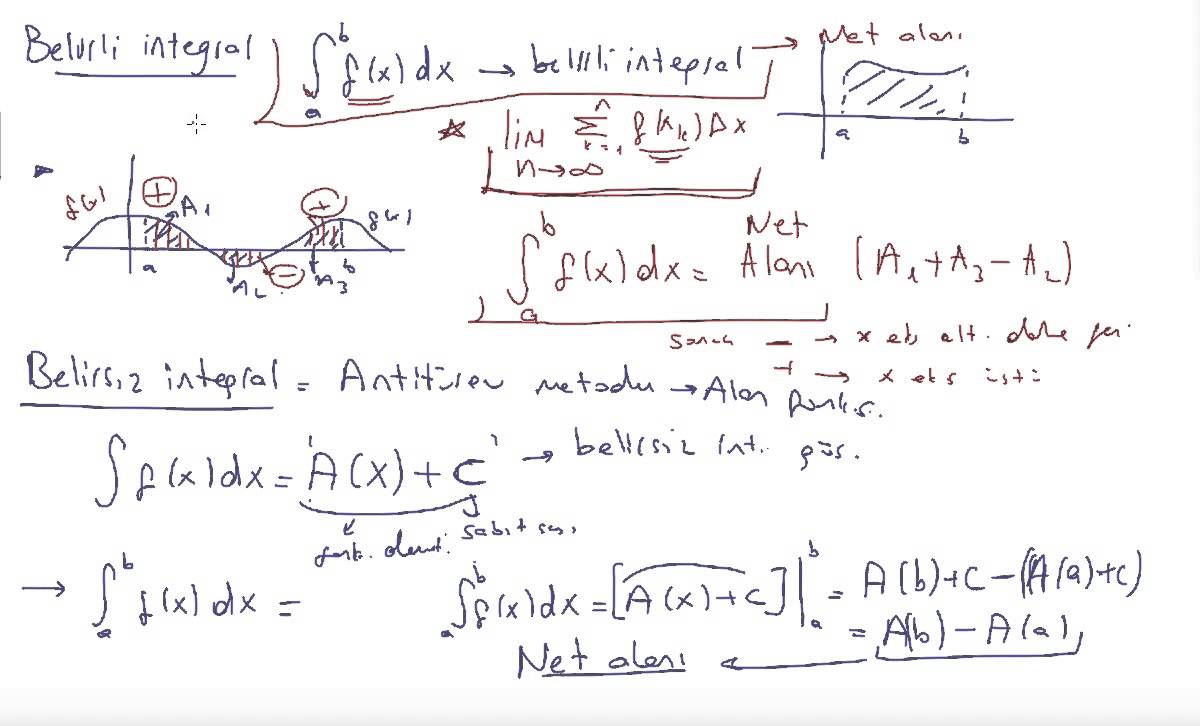
I.1.Belirsiz İntegralin Tanımı: Türevi f(x) olan bir F(x) fonksiyonuna f(x)’in ilkel fonksiyonu ve diferansiyeli f(x)dx olan F(x) fonksiyonunda f(x)dx ‘in belirsiz integrali denir.
dF(x) = f(x)dx veya =f(x)
İse
F(x) = ∫ f(x)dx
Dir. Genel olarak:
∫ f(x)dx = F(x) + c
dir. Buradaki C keyfi sabittir.

I.2 BAŞLICA İNTEGRAL TEOREMLERİ VE İNTEGRAL TABLOSU

u ve v(x)’in fonksiyonları: a,b,c sabitler olmak üzere aşağıdaki eşitlikler yazılabilir.
1 ∫ df(x) = f(x) + c
2 ∫ d f(x) = f(x)dx
3 ∫ odx = c
4 ∫ a f(x)dx = a ∫f(x)dx
5 ∫ (u + v +w + …)dx = ∫ udx + ∫vdx + ∫wdx + …
6 ∫ udv = uv –∫ vdu
7 ∫ = dx = uv- ∫v dx
8 ∫ f(y)dx = ∫
9 ∫ du =
10. ∫ = logu + c
11 ∫ du =
12 ∫ audu =
13 ∫ sinudu = – cosu + c
14 ∫ cosudu = sinu + c
15 ∫ tgudu = logsecu + c = -logcosu + c
16 ∫ cotgudu = logsinu + c
17 ∫ secudu = log (secu + tgu) + c = log + g ( + c
18 ∫ cosecudu = log (cosecu – cotgu) + c = log + g + c
19 ∫ udu = u + sin u cos u + c = u – sin 2u + c
20 ∫ udu = u + sin u cosu + c = u + sin 2u + c
21 ∫ udu + tgu + c
22 ∫ udu = – cotgu + c
23 ∫ udu = tgu – u+c
24 ∫ udu = -cotgu – u + c
25 ∫ = arctg + c
26 ∫ = log ( ) + c
27 ∫ = arcsin + c
28 ∫ = log (u + ) + c
29 ∫ = log (u + ) + c
30 ∫ du = .arcsin + c
31 ∫ .du =–
32 ∫
33 ∫ shudu = chu + c
34 ∫ chudu = shu + c
35 ∫ thudu = log (chu) +c

I.3. İNTEGRAL ALMA YÖNTEMLERİ

Değişken Dönüştürme Yöntemleri
Değişken dönüştürümü yardımıyla integral hesabı yöntemi diferensiyelin ifadesinin seçilen değişkene bağlı olmaması özelliğine dayanır.
Bu yöntem,
f(x)dx
integralini x değişkenine
x = g(t)
Denklemi ile bağlı olan yeni bir t değişkenin fonksiyonu olarak ifade etmekten ibarettir.
g(t) nin sürekli bir (t) türevinin olduğu varsayılarak,
f(x)dx = f [g(t)] (t)dt
Olduğundan,
∫ f(x)dx = ∫ f[g(t)] (t)dx yazılır.
Hesaplanması istenilen bir belirsiz integral , uygun bir değişken dönüştürümü ile bilinen bir
şekle sokulursa, integral yeni t değişkeni cinsinden elde edilir. Sonucu x cinsinden ifade etmek
için, x = g(t) bağıntısından t çözülerek sonuçta yerine koymak yeterlidir.
ve ti ihtiva eden İntegraller :
halinde x = t sin ℓ veya x= t.cos ℓ
halinde x = t.sec ℓ
halinde x = t tg ℓ

değişken dönüştürmeleri yapılır.

I.3.2 Kısmi İntegrayon Yöntemi:

U ve v ile, x’in bir [a,b] aralığında sürekli türevleri olan iki fonksiyonunu gösterelim.
uv çarpımının diferensiyeli
d(uv) = udv + vdu ‘ dır. Buradan
udv=d(uv)-vdu
yazılır. Bu bağlantının iki tarafının belirsiz integralleri birbirine eşittir:
∫udv = ∫d(uv) – vdu veya
∫udv = uv – ∫vdu ‘ dur.
Kısmi integrasyon metodu bu formül ile verilmiştir ve yöntemin esası hesaplanması istenilen
∫ udv yerine hesaplanması daha kolay olabilen
∫ vdu belirsiz integralini kaymayı mümkün kılar.

II. BELİRLİ İNTEGRAL

II.1 Belirli İntegralin Tanımı: f(x) , x = a dan x = b’ye kadar olan aralıkta sürekli bir fonksiyon olsun. Bu aralığı , apsisleri a, ,….,xn – 1, b olan n parçaya bölelim. Aralıkların boyları,
, …. , ∆xn olsun. Bu aralıkların her birinde x’in x’1, x’2 , x3’…., x’n gibi herhangi
değerleri alalım f(x)’in x = a , x=b imitleri arasındaki belirli integrali diye:
f(x) dx = ℓim f(x 😉 ∆x, + ℓ( ’) x2+… + f( 1)
n→ 8

= ℓim ∑ f(xi1) xi
n→ 8
=| ∫ f(x) dx| b = F(x) b = F(b) – F(a)
Ya denir. Buradaki F(x) fonksiyonu türevi f(x) olan bir fonksiyondur.

II.2.Belirli İntegrale Ait Başlıca Teoremler

B f1(x) + f2(x) +….+ fn (x) dx= f1 (x) dx + b f2(x) dx +…+ b fn (x) dx
k.f (x) dx = k. B f(x) dx
f (x) dx = – a f(x) dx
f(x) dx = c f(x) dx + b f(x) dx
f(x) dx = (b-a)f(x1)
f(x)dx = Lism f(x) dx

Not: Alıntıdır.